こんにちは、フルーツポンチです。
今回は最近はまっている、関数をもとにしたグラフによるアートについてです。

まず、こちらをご覧ください。

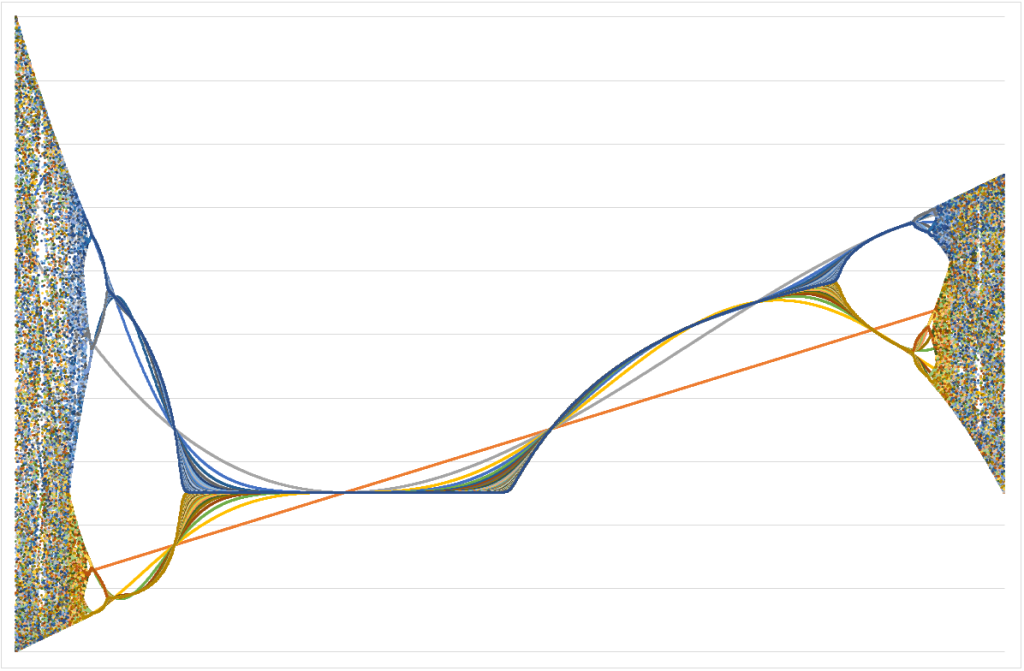
このような形で、Excelなどを使用して関数の結果を出力したりするのにはまっています。

今回使用した関数は”ロジスティック写像”と呼ばれるもので、比較的単純な式ながら、結果が複雑なものになるものです。
グラフによるアートにはまったのも、ロジスティック写像のWikipediaの記事を見て面白そうだと思ったからなので、まずこれから紹介したいと思いました。
上の画像では、変数の初期状態を0.8として、定数を-2から4の範囲で出力したものを、散布図で出力したものです。

今回は計算のやり方としてPowerQueryを使っていて、以下のような計算用のカスタム関数で計算した結果を整形して使用しています。

(paramB as number, paramT as number, paramInc as number, varInit as number, plotCount as number) =>
let
　　paramRange = List.Generate(
　　　　　　　　　　 () => paramB,
　　　　　　　　　　 each _ <= paramT,
　　　　　　　　　　 each _ + paramInc),
　　calcMath = List.Transform(
　　　　　　　　　 paramRange,
　　　　　　　　　 each [
　　　　　　　　　　　 Param = _,
　　　　　　　　　　　 Plot = List.Skip(
　　　　　　　　　　　　　 List.Generate(
　　　　　　　　　　　　　　　 () => [
　　　　　　　　　　　　　　　　　 Count = 0,
　　　　　　　　　　　　　　　　　 Value = varInit
　　　　　　　　　　　　　　　 ],
　　　　　　　　　　　　　　　 each _[Count] <= plotCount,
　　　　　　　　　　　　　　　 (nowVar) => [
　　　　　　　　　　　　　　　　　 Count = nowVar[Count] + 1,
　　　　　　　　　　　　　　　　　 Value = nowVar[Value] * _ * (1 - nowVar[Value])
　　　　　　　　　　　　　　　 ],
　　　　　　　　　　　　　　　 each _[Value]),
　　　　　　　　　　　　　 1)
　　　　　　　　　 ]),
　　toTable = Table.FromRecords(calcMath)
in
　　toTable

paramBを定数の下限、paramTを定数の上限、paramIncを定数の増加単位、varInitを変数の初期値、plotCountを一つの定数毎に出力する点の数としていて、1つ目の例ではparamBを-2、paramTを4、paramIncを0.002、varInitを0.8、plotCountを100と指定しています。

他にも、値やグラフの種類・設定を変えることで以下のような出力もできました。

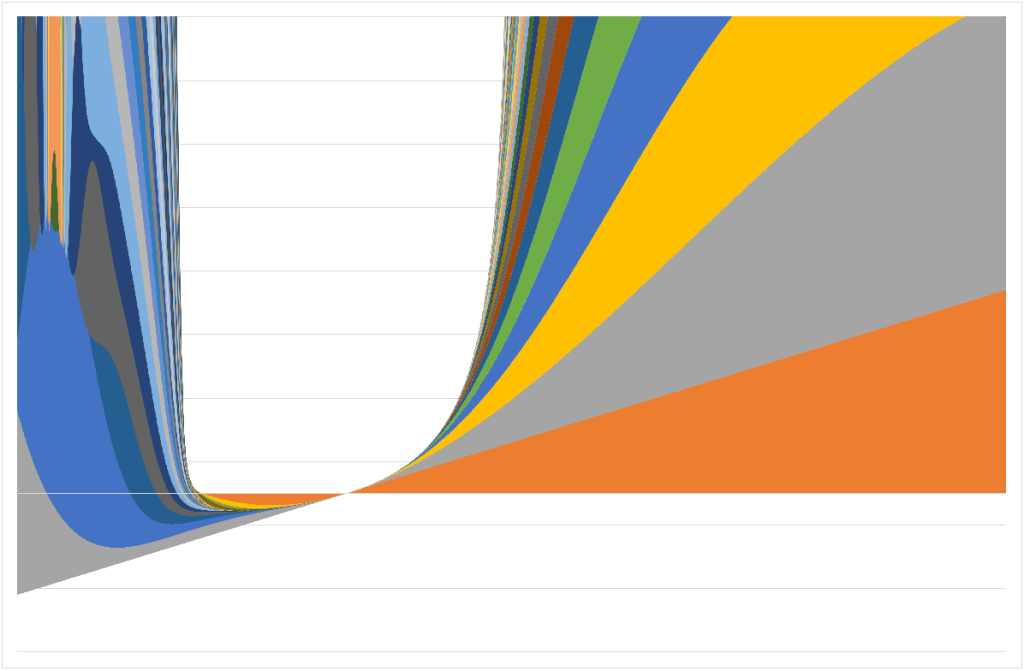
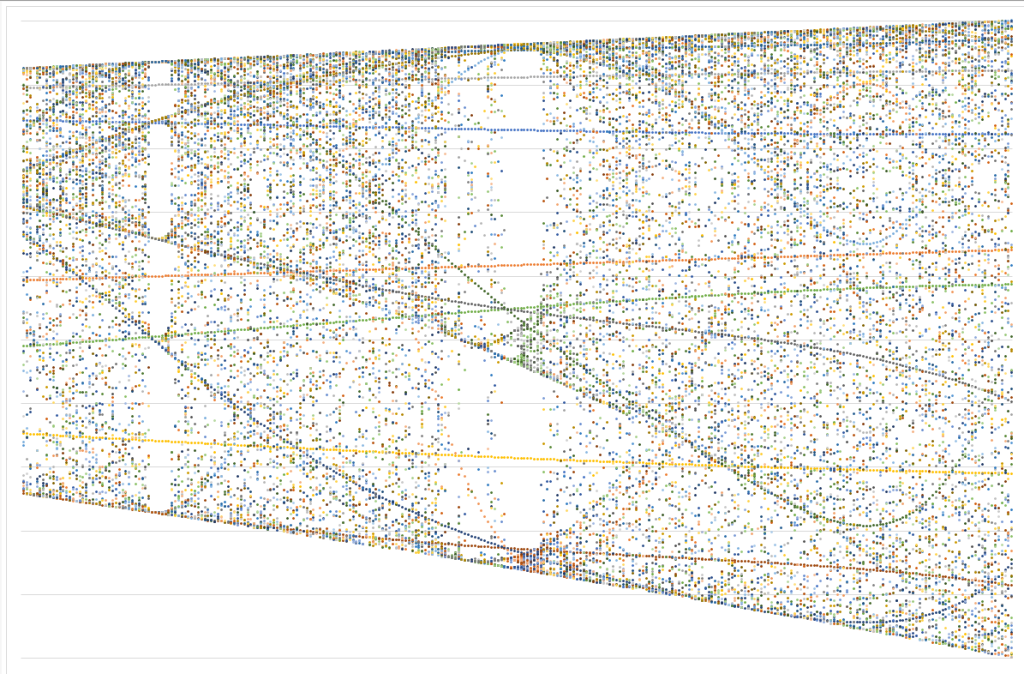
個人的には4つ目の画像がお気に入りで、中央付近に4本の線が交差している箇所が特にお気に入りです。

最後に、私はこういった関数などについてはあまりわからず、実際に使用しているカスタム関数の内容があっているのかはわかりませんが、それっぽくしても面白い結果になるので、敷居はあまり高くないと思います。
なので、一度こういったアートなどに挑戦してみるのも面白いと思います。